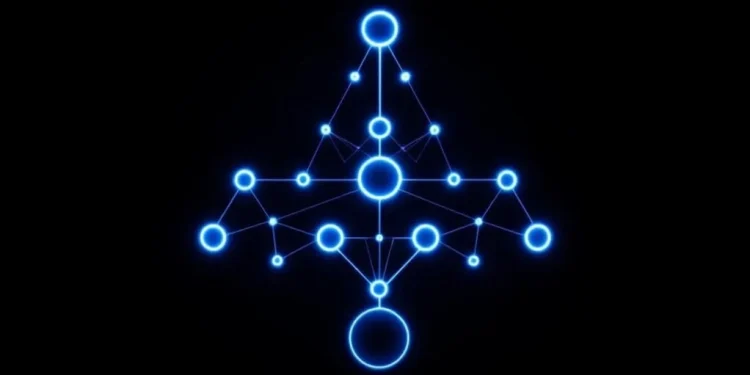
A segment tree is a data structure that stores array elements in a binary tree format to handle range-based operations efficiently. It enables fast queries and updates across multiple elements by organizing data hierarchically. The root node represents the entire array, while leaf nodes contain individual elements. This structure allows operations like finding sums, minimums, or maximums within ranges in logarithmic time, making it valuable for computational tasks that require frequent range calculations.

A segment tree is a specialized data structure used to handle range queries on arrays efficiently. It’s designed as a binary tree where each node represents an interval or segment of an array. The root node covers the entire array, while leaf nodes represent individual elements. This structure makes it particularly useful for operations that need to process ranges of data quickly.
The tree’s organization follows a simple principle: each internal node has two children that represent half of their parent’s interval. For example, if a parent node represents positions 0 to 7 in an array, its children would represent positions 0 to 3 and 4 to 7. This hierarchical structure continues until reaching individual elements at the leaf nodes. The data structure enables efficient retrieval of segments containing any query point. Each node stores a value computed through merge operations during construction, ensuring efficient range calculations.
One of the key strengths of segment trees is their efficiency in both querying and updating data. They can perform operations like finding the sum, minimum, or maximum of elements within a specific range in logarithmic time, specifically O(log n), where n is the number of elements. This makes them much faster than simple array traversal for range operations. Following DRY principles helps maintain consistency in segment tree implementations.
Segment trees revolutionize range operations with logarithmic efficiency, outperforming traditional array traversal for sum, minimum, and maximum calculations.
The construction of a segment tree requires O(n) storage space and can be completed in O(n log n) time. While this initial setup might seem costly, it pays off when multiple range queries or updates are needed. The total number of nodes in a complete segment tree is 2N – 1, where N is the number of elements in the original array.
Segment trees find applications across various fields in computer science. They’re commonly used in computational geometry for spatial queries, in geographic information systems for analyzing spatial data, and in machine learning for efficient data processing. Their ability to handle both queries and updates efficiently makes them valuable in real-time applications.
The structure supports several essential operations. Users can query ranges to find sums, minimums, or maximums, update individual elements, or modify entire ranges of values. Each of these operations maintains the tree’s efficiency, making it a reliable choice for scenarios requiring frequent range-based calculations.
What makes segment trees particularly valuable is their balanced performance in both querying and updating operations. They scale well with large datasets due to their logarithmic time complexity and provide flexibility in handling different types of range-based problems. This combination of efficiency and versatility has made them a fundamental tool in modern algorithmic applications.
Frequently Asked Questions
How Does Segment Tree Performance Compare With Other Data Structures?
Segment trees outperform arrays and linked lists in range queries, operating in O(log n) time. While balanced BSTs offer similar efficiency, segment trees excel specifically at range-based operations.
Can Segment Trees Handle Negative Numbers in the Input Array?
Segment trees can effectively handle negative numbers in input arrays without requiring modifications. The data structure maintains its O(log n) performance for operations regardless of value signs.
What Are the Memory Requirements for Implementing a Segment Tree?
A segment tree requires either 4n memory (standard allocation) or 2n-1 memory (optimal allocation), where n is the input size. Sparse implementations use dynamic memory based on active nodes only.
Is It Possible to Modify Segment Trees for 2D Array Operations?
Yes, segment trees can be modified for 2D array operations through 2D segment trees, which implement nested segment trees or create separate trees for each dimension/row.
When Should I Choose Segment Trees Over Binary Indexed Trees?
Segment trees are preferred when non-cumulative operations or diverse range queries are needed, while binary indexed trees suit cumulative operations. Segment trees offer more flexibility despite higher implementation complexity.