A Binary Tree is a hierarchical data structure in computer science where each node possesses up to two children, termed the left and right child. It is instrumental in efficient data storage, retrieval, and manipulation across various programming languages. There are diverse types, including Full, Complete, Perfect, Degenerate, and Skewed Binary Trees, differing by node configurations and properties. Node representation techniques focus on maintaining connectivity, and operations include insertion, deletion, traversal, and balancing to optimise tree performance.
Main Points
- A binary tree is a hierarchical data structure with each node having at most two children: left and right.
- It’s instrumental for efficient data storage, retrieval, and manipulation, supporting insertion, deletion, and traversal operations.
- Depending on their structure, ■ Binary trees can be of different types, including complete, total, perfect, degenerate, or skewed.
- The storage methods of binary trees involve node representation techniques and can be either sequential (using arrays) or linked (using pointers).
- Binary trees are widely used in programming due to their unique structure that optimises data operations.
Understanding Binary Tree Basics
To fully understand a binary tree, it is essential to explore the fundamental principles that define their distinctive hierarchical structure and diverse functionality. A binary tree is a type of tree data structure in which each node has at most two children, referred to as the left child and the right child. This configuration is instrumental in creating a hierarchical order that supports efficient data storage, retrieval, and manipulation.
A binary tree structure enables the implementation of critical operations such as insertion, deletion, and traversal with relative ease. Nodes in a complete binary tree have either two children or none, ensuring a uniform structure. However, nodes in a binary tree can also have fewer children, leading to various tree structures.
A balanced binary tree, on the other hand, maintains an optimised structure by ensuring that the height difference between the left and right subtrees of any node is not more than one. This balance enhances the speed of operations, contributing to the binary tree’s widespread application in algorithms and data structures.
Different Types of a Binary Tree
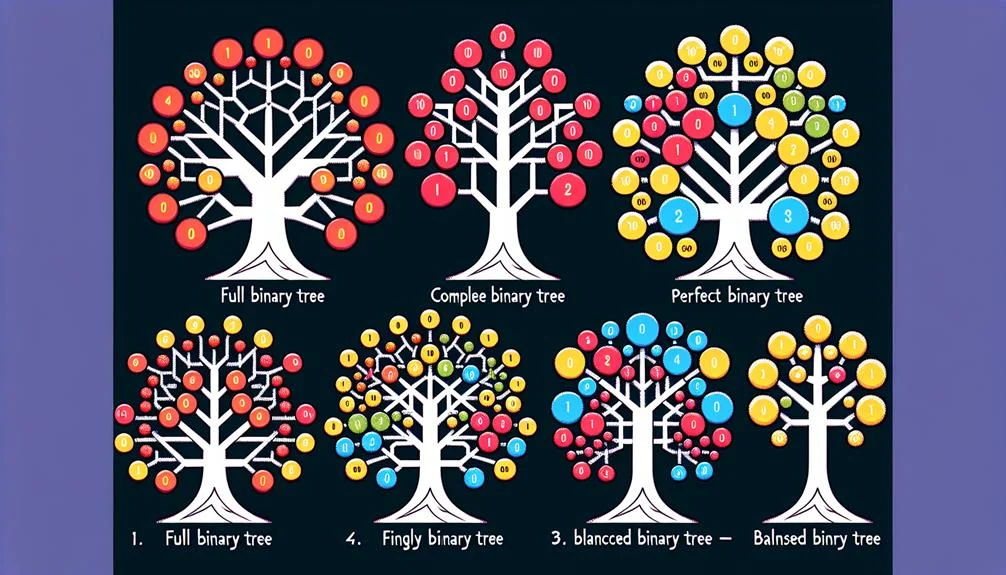
Binary trees are categorised into five primary types: complete, full, perfect, degenerate (or pathological), and skewed binary tree. Each type possesses unique properties and structural configurations.
A complete binary tree is distinguished by its filled levels, with leaf elements leaning towards the left. Opposing this structure, full binary trees have a parent node with either two children or none.
Perfect Binary Trees take a balanced approach, with each internal node having precisely two children and all leaf nodes existing at the same level. Contrastingly, a Degenerate (or Pathological) Tree simplifies the structure, presenting a single child either left or right.
Lastly, the Skewed Binary Tree favours one direction, with the tree being dominated by either left nodes or right nodes. This type includes both left-skewed and right-skewed variations.
To summarise:
- Complete binary tree: every level completely filled, leaf elements towards the left.
- Full binary trees: parent node has two or no children.
- Perfect Binary Tree: every internal node has two child nodes, and all leaf nodes are at the same level.
- Degenerate (or Pathological) Tree: a single child either left or right.
- Skewed Binary Tree: dominated by either left nodes or right nodes.
Properties of a Binary Tree
In computer science, binary trees demonstrate a set of distinct properties that govern their structure and functionality, which is essential for understanding their operation and utilisation in data management and algorithms. Each node in a binary tree possesses a maximum of two children, commonly referred to as the left and right child. This bifurcation is a fundamental attribute, defining the binary nature of the tree.
Evaluating the depth and height of a binary tree is achieved by measuring the length of the longest path from the root to a leaf node. These metrics are vital in appraising the tree’s structure and performance during data manipulation and search operations.
A binary tree’s full and complete states contribute significantly to its efficiency and balance. A complete binary tree is one where each node has either zero or two children, facilitating a balanced framework for algorithmic processes. On the other hand, a full binary tree guarantees all levels are filled, except potentially the last. This property maintains a structured hierarchy, optimising data storage and retrieval.
Storage Methods of a Binary Tree
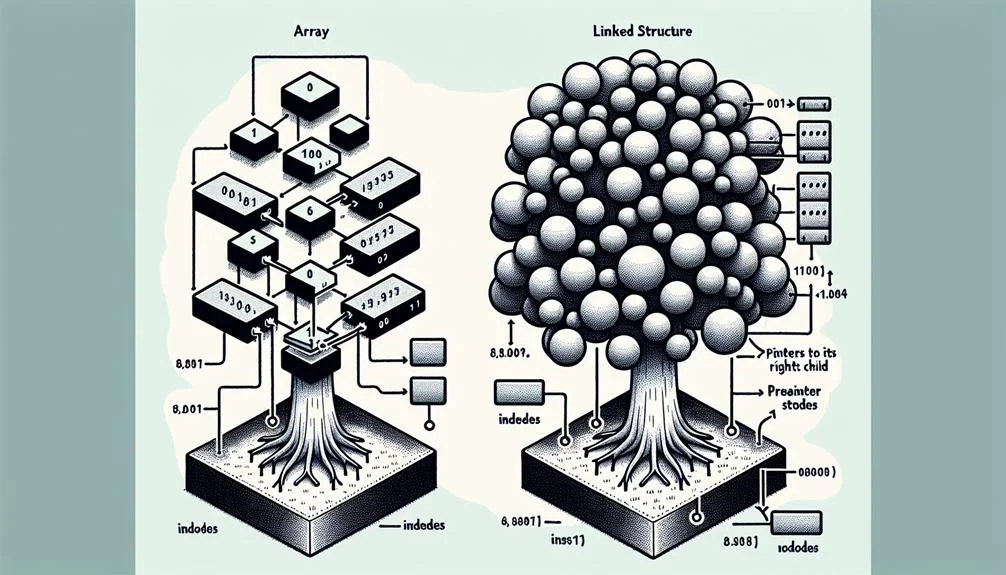
In examining binary tree storage methods, two primary techniques surface: node representation and the choice between sequential versus linked storage. Node representation involves allocating data and pointers to child nodes in each parent node, an essential aspect of tree manipulation.
On the other hand, the decision between sequential or linked storage can considerably impact factors such as storage efficiency and traversal speed, thereby influencing data retrieval processes.
Node Representation Techniques
A critical aspect of binary trees pertains to the techniques employed in node representation, which typically involve storing data along with pointers to the left and right child nodes. This structure enables an efficient hierarchical organisation within the binary tree, facilitating streamlined navigation and manipulation.
Node representation techniques often include:
- Utilising structures in programming languages, which comprise data fields and pointers.
- Ensuring each node consists of data elements and references to child nodes for hierarchical organisation.
- Employing pointer-based storage to enhance the traversal and manipulation of binary tree structures.
- Ensuring proper node representation to maintain cohesive connectivity within the binary tree data structure.
Thus, the efficient representation of nodes is fundamental to the operation and utility of binary trees.
Sequential Versus Linked Storage
How best to store data in binary trees?
This question leads us to two primary methods: sequential and linked storage, each with unique characteristics and use cases. Sequential storage represents binary trees using arrays, permitting efficient random access to nodes via index calculations. However, it’s not without drawbacks. The maximum number of nodes is fixed, leading to potential memory wastage with sparse trees.
Contrastingly, linked storage capitalises on pointers to dynamically connect nodes, enabling efficient memory usage and flexible tree modifications. This method excels in scenarios requiring dynamic tree modifications but lacks the random access convenience of sequential storage.
The choice depends on the specific requirements of the binary tree implementation.
Common Operations of a Binary Tree
Understanding the intricacies of joint operations on binary trees, such as insertion, deletion, traversal, searching, and balancing, is crucial for optimising data storage and retrieval. These operations, performed on a structure where each tree consists of three components: a node value, a left child, and a right child, allow for effective data organisation.
- Insertion: This operation involves adding a new node to the binary tree. The placement of the new node is determined by the tree’s existing structure and the number of internal nodes. This operation takes into consideration the height of the tree to maintain balance.
- Deletion: Nodes with zero or one child can be removed without disrupting the tree’s structure. The leaf nodes are typically targeted for removal to maintain consistency.
- Traversal: Pre-order and post-order traversal are standard tree navigation techniques. Pre-order traversal visits the root first, then the left subtree and finally the right subtree. Post-order traversal visits the left subtree, the right subtree, and then the root.
- Balancing: The tree is periodically balanced to guarantee efficient data access. This operation reorganises the nodes to minimise the tree’s height and optimise retrieval time.
A Binary Tree in Programming Languages

Frequently utilized in various programming languages, binary trees are hierarchical data structures that provide efficient methods for data storage, retrieval, and manipulation, with each node containing references to at most two children – the left and right child. The robustness and versatility of binary trees have made them fundamental elements in algorithms and data structures, adding to their wide use in different programming languages.
Each node in a binary tree is a unique entity that holds data and provides pathways, or references, to its left and right children. This guarantees efficient traversal and manipulation of the data structure. Implementing binary trees in programming languages involves defining the structure and properties of these nodes and managing tree operations such as insertion, deletion, and search.
In programming languages, binary trees are not just a conceptual abstraction. They are practical, invaluable data structures that transform how data is stored, retrieved, and manipulated. Their unique structure, consisting of a parent node and, at most, two children, facilitates efficient data operations, making binary trees a staple in every programmer’s toolkit.
Binary Trees used in Algorithms
A binary tree is a hierarchical data structure composed of nodes, where each node has at most two children: a left child and a right child. Binary trees are commonly used in algorithms and applications due to their efficient structure. Here’s how they work:
- Node Structure: Each node in a binary tree contains a value and pointers to its left and right children.
- Root Node: The topmost node of the tree is called the root node.
- Child Nodes: Nodes directly connected to another node are its children. Each node can have at most two children, a left child, and a right child.
- Traversal: Algorithms can traverse binary trees in different ways:
- Inorder: Left, Root, Right
- Preorder: Root, Left, Right
- Postorder: Left, Right, Root
- Searching: Binary trees are used in searching algorithms, particularly in binary search trees (BST), where each node’s value is greater than all values in its left subtree and less than all values in its right subtree.
- Insertion and Deletion: Algorithms can insert and delete nodes while maintaining the binary tree’s properties, such as maintaining the BST property in binary search trees.
Binary Tree Interview Questions

Binary tree interview questions is essential to technical job interviews, as they demonstrate the interviewee’s mastery over binary tree operations and properties. These questions probe the depth of an individual’s understanding of how a tree is a binary structure and their ability to manipulate it using techniques such as tree traversal, insertion, deletion, and balancing.
To make this discussion more thorough, here are some key areas that binary tree interview questions may cover:
- Tree Traversal Methods: Understanding different traversal methods, like in-order, pre-order, and post-order, are essential.
- Insertion and Deletion Operations: Proficiency in inserting and deleting nodes in a binary tree is crucial.
- Balancing a Binary Tree: Mastery over techniques to balance a binary tree, such as AVL and Red-Black trees, is often tested.
- Problem-solving Skills: The ability to solve complex problems related to binary trees demonstrates solid problem-solving skills and coding and algorithm skills.
Therefore, proficiency in these areas can significantly improve a candidate’s performance in technical interviews, showing a deep understanding of binary trees.
Conclusion
To summarise, binary trees are fundamental data structures in computer science, providing efficient storage and retrieval methods. These trees have various types and properties and are utilised in different programming languages.
Understanding binary trees is essential, as they are frequently used in interviews and practical applications. Intriguingly, a perfect binary tree can sort 1 million numbers in less than 20 milliseconds, highlighting their importance in efficient data management.





